ESM Welcomes College MatchPoint to the Team! Learn More

What geometry actually shows up on the ACT or the SAT?
Sometimes geometry questions on the ACT and SAT look really intimidating, especially if you’ve recently had to write a proof and lost points because of the difference between the Corresponding Angles Theorem and the Converse of the Corresponding Angles Theorem.
Geometry proofs can feel long winded and nitpicky, and so a geometric figure on the ACT or SAT can trigger nerves. However, you only need to know a few formulas and concepts. Most geometry questions boil down to those foundation concepts, and if they look trickier, you probably need to add a line and spot a triangle.
So what do you have to know in order to get geometry questions right on the ACT and SAT?
The SAT provides this information on the cover page of each math section:
2D:
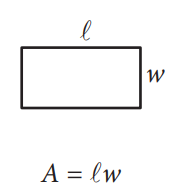
3D:
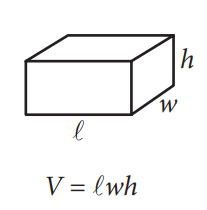
The ACT doesn’t provide that information, so you should have that foundation knowledge down.
You don’t need to memorize the following formulas. Sketch a picture of the scenario and use logic rather than memorizing more formulas.
$$P \; = \; 2l \; + \; 2w$$
$$SA \; = \; 2lw \; + \; 2lh \; + \; 2wh$$
Applications of Pythagorean Theorem:
Rectangles are full of right angles, so if you need other information in a question (like the length of a diagonal), chances are you need to draw a line and spot a right triangle and apply Pythagorean Theorem or a Special Right Triangle ratio.
The equation of a circle in the \(xy\)-plane with center \((h,k)\) is \((x−h)^2 \; + \; (y−h)^2 \; = \; r^2\).
Yes, please memorize this one.
It is basically the Pythagorean Theorem and both tests love to toss in a question with this one without giving you the formula.
The SAT provides this information on the cover page of each math section:
YES, these do show up on every test:
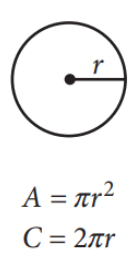
Meh, this might show up on a test:
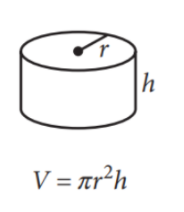
Occasionally helpful:
Right angles are awesome, and congruent line segments are also awesome. In a figure, if you really suspect an angle is a right angle, then it probably is, and if you really suspect two segments are congruent, then they probably are.
Here are a couple geometry facts to help support that gut instinct about right angles:
If you’re not sure what to do on a circle question, draw radii until you spot triangles. Hopefully you’ll spot a right triangle or an isosceles triangle which can be chopped into congruent right triangles. Basically, right triangles are bosses.
If you need this information on a question, these formulas will be provided:
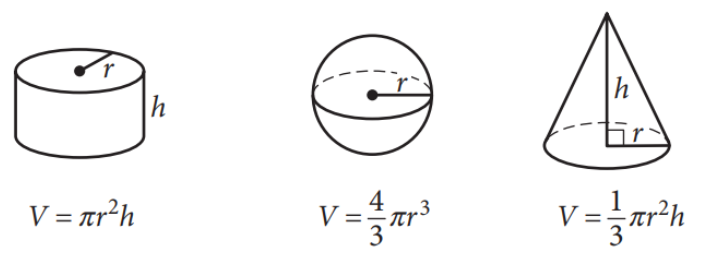
Honestly, the SAT provides these on the cover page but almost never uses them. The ACT might have a sphere or cone question every once in a while, and they will provide the formulas.
(Note: The ACT will most likely include a formula like those in a note in parentheses under the question and above the answer choices.)
Triangles are the boss of geometry questions. Know how to work with triangles and you’re in charge. If you see an intimidating geometric figure, add lines until you spot triangles.
The SAT provides this information on the cover page of each math section:
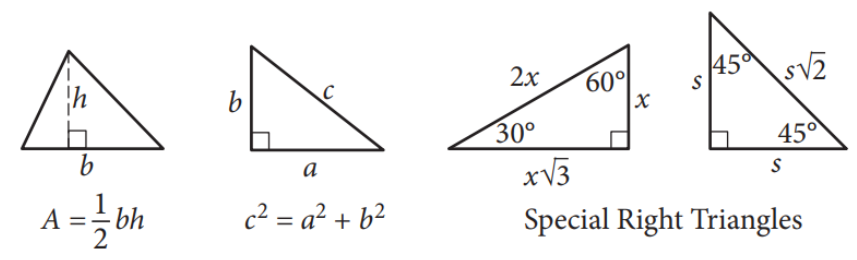
Those are expected knowledge and they do help on every test. Notice how many right angle symbols you see in those reference formulas.
Right angles are great! In a right triangle, you also have the trigonometric functions:
$$\sin{(\text{acute angle})} = \frac{(\text{leg opposite from that angle})}{hypotenuse}$$
$$\csc{(\theta)} = \frac{1}{\sin{(\theta)}}$$
$$\cos{(\text{acute angle})} = \frac{(\text{leg adjacent to that angle})}{hypotenuse}$$
$$\sec{(\theta)} = \frac{1}{\cos{(\theta)}}$$
$$\tan{\text{(acute angle})} = \frac{(\text{leg opposite from that angle})}{(\text{leg adjacent to that angle})}$$
$$\cot{(\theta)} = \frac{1}{\tan{(\theta)}}$$
(Note (1): \(\sin^{-1}{(\text{ratio})} = \text{angle}\) is not the same thing as \(\frac{1}{\sin{(\text{angle})}}\). You have a button on your calculator for \(\sin\) and an option for \(\sin^{-1}\), but will need to type \(\frac{1}{\sin{(\text{number})}}\) if you want \(\csc{(\text{number})}\).)
(Note (2): The hypotenuse is always the longest side, opposite from the 90°, while the legs are labeled as “opposite” or “adjacent” depending on which acute angle you’re considering.)
When you have a trig function, you should have a voice in your head reminding you to double check whether you are operating in degree mode or radian mode. On the ACT, this affects how you use your calculator to test values in expressions or to solve for angles or lengths. On the SAT, you’re more likely to encounter a one-off question involving converting between radians and degrees, and the SAT does provide this on the cover page, hidden under the other formulas where it’s easy to miss it:
If you spot Pythagorean Triples (sets of integers that satisfy the Pythagorean Theorem), you can make really short work of some questions.
Most common:
3:4:5
Example:
You have a right triangle. One leg is 0.6 and the hypotenuse is 1. You can conclude that the other leg is 0.8 without having to set up and solve \(a^2+b^2=c^2\) if you spot that it’s a 3:4:5, scaled by 0.2.
Less common but still helpful:
5:12:13
7:24:25
8:15:17
You DO NOT need to know the definition of medians of a triangle and their point of concurrency, the centroid; perpendicular bisectors of a triangle and their point of concurrency, the circumcenter; angle bisectors of a triangle and their point of concurrency, the incenter; or
altitudes of a triangle and their point of concurrency, the orthocenter in order to answer any geometry question on either the ACT or the SAT.
You DO NOT need to know the other area formulas for a triangle, but I have seen one of these make short work of one question on one ACT once:
$$A=\frac{1}{2} ab \sin{(C)}$$ $$A=\sqrt{s(s-a)(s-b)(s-c)}, \text{ where } s=\frac{a+b+c}{2}$$
If you have any questions or would like help working through some practice questions to see if you got all that, I’d love to hear from you. Feel free to send me an email at BAdams@esmprep.com.